$ \newcommand\define[1]{\textbf{#1}\index{#1}} % Letters/Font \DeclareMathOperator{\F}{\mathbb{F}} \DeclareMathOperator{\bF}{\mathbb{F}} \DeclareMathOperator{\Q}{\mathbb{Q}} \DeclareMathOperator{\bQ}{\mathbb{Q}} \DeclareMathOperator{\Z}{\mathbb{Z}} \DeclareMathOperator{\bZ}{\mathbb{Z}} \DeclareMathOperator{\R}{\mathbb{R}} \DeclareMathOperator{\bR}{\mathbb{R}} \DeclareMathOperator{\C}{\mathbb{C}} \DeclareMathOperator{\bC}{\mathbb{C}} \DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\bE}{\mathbb{E}} \DeclareMathOperator{\N}{\mathbb{N}} \DeclareMathOperator{\bN}{\mathbb{N}} \DeclareMathOperator{\M}{\mathbb{M}} \DeclareMathOperator{\mM}{\mathbb{M}} \DeclareMathOperator{\bH}{\mathbb{H}} \DeclareMathOperator{\bP}{\mathbb{P}} \DeclareMathOperator{\cH}{\mathcal{H}} \DeclareMathOperator{\cA}{\mathcal{A}} \DeclareMathOperator{\cB}{\mathcal{B}} \DeclareMathOperator{\cC}{\mathcal{C}} \newcommand\bb[1]{\mathbb{#1}} \newcommand\mc[1]{\mathcal{#1}} \newcommand{\w}[1]{\wedge#1} \newcommand\mean[1]{\bar{#1}} \newcommand\conj[1]{\bar{#1}} % Grouping Operators \newcommand{\floor}[1]{\left\lfloor#1\right\rfloor} \newcommand{\ceil}[1]{\left\lceil#1\right\rceil} \newcommand{\parens}[1]{\left(#1\right)} % note that we defined bracks not brace/braces because brace is already used by amsmath \newcommand{\bracks}[1]{\left\{#1\right\}} \newcommand{\sqbracks}[1]{\left[#1\right]} \newcommand{\clop}[1]{\left[#1\right)} \newcommand{\opcl}[1]{\left(#1\right]} \newcommand{\angles}[1]{\langle#1\rangle} % probability \DeclareMathOperator{\Cov}{Cov} \DeclareMathOperator{\Var}{Var} \DeclareMathOperator{\median}{median} % https://tex.stackexchange.com/questions/154530/resolved-a-conditional-independence-symbol-that-looks-good-with-mid \newcommand{\indep}{\mathrel{\text{\scalebox{1.07}{$\perp\mkern-10mu\perp$}}}} \newcommand{\norm}[1]{\left\lVert#1\right\rVert} % linear algebra \DeclareMathOperator{\rank}{rank} \DeclareMathOperator{\nullity}{nullity} \DeclareMathOperator{\rowrank}{row rank} \DeclareMathOperator{\colrank}{column rank} \DeclareMathOperator{\tr}{Tr} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\perm}{perm} \DeclareMathOperator{\GL}{GL} \DeclareMathOperator{\imm}{imm} \DeclareMathOperator{\poly}{poly} % abstract algebra \DeclareMathOperator{\Aut}{Aut} \DeclareMathOperator{\id}{id} \DeclareMathOperator{\Inn}{Inn} \DeclareMathOperator{\irr}{irr} \DeclareMathOperator{\Frac}{Frac} \DeclareMathOperator{\Frob}{Frob} % category theory \DeclareMathOperator{\ob}{ob} \DeclareMathOperator{\Set}{Set} \DeclareMathOperator{\Grp}{Grp} \DeclareMathOperator{\Ring}{Ring} \DeclareMathOperator{\Top}{Top} \DeclareMathOperator{\Vect}{Vect} \DeclareMathOperator{\End}{End} \DeclareMathOperator{\Hom}{Hom} \DeclareMathOperator{\im}{im} \DeclareMathOperator{\op}{op} % number theory \DeclareMathOperator{\rad}{rad} \DeclareMathOperator{\Disc}{Disc} \DeclareMathOperator{\res}{res} % differential geometry \DeclareMathOperator{\Man}{Man} $

Word Game（文字遊戲）Locks Puzzle Analysis

Published: 24 Apr 2022

Last updated: 24 Apr 2022

Categories Tags

I’ve been playing Word Game/文字遊戲 recently, and I ran into a puzzle that made me ask some questions about generators of the symmetric group \(S_7\)!

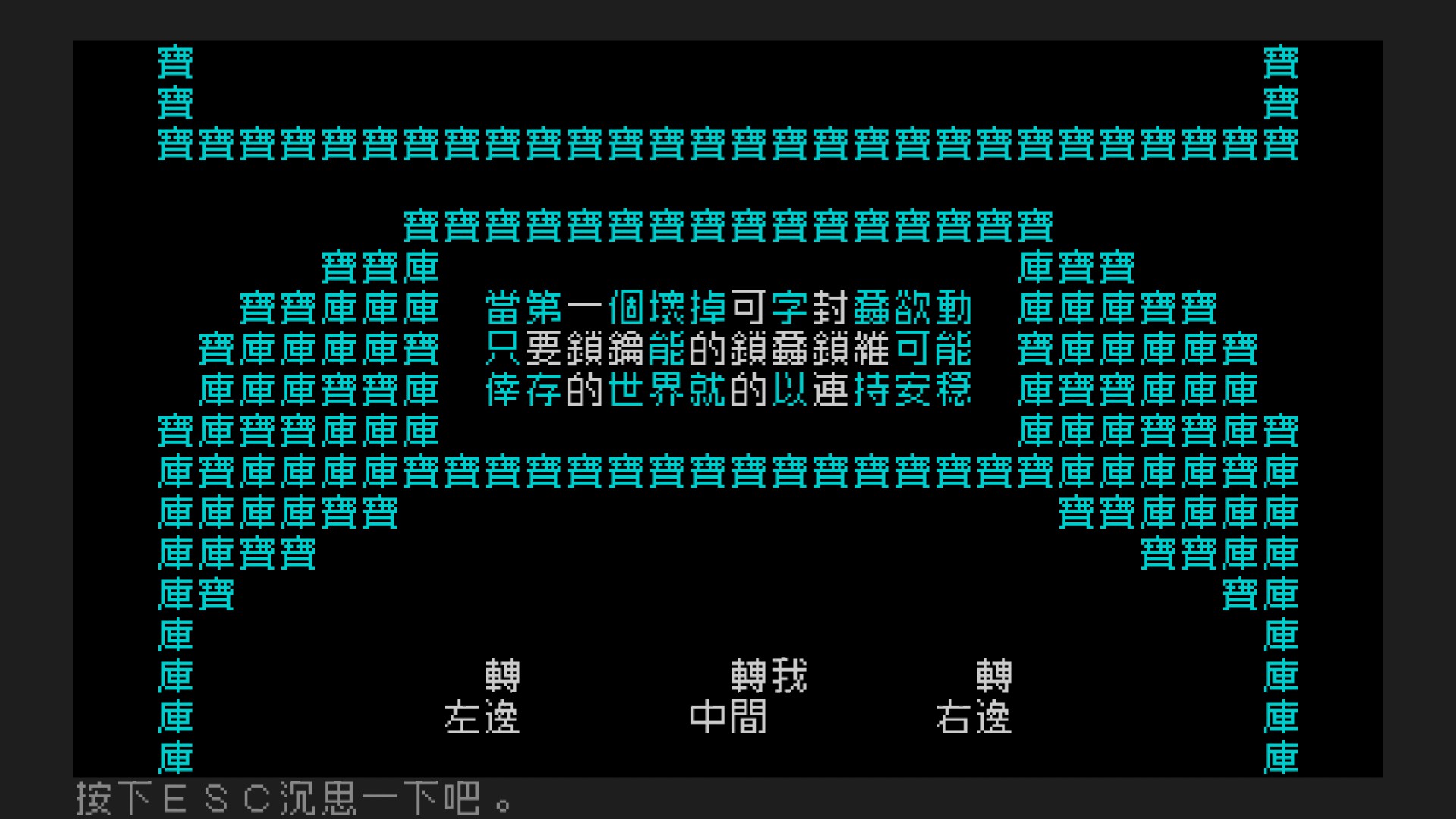
Start

End

You have to press the 轉 characters to rotate the four characters surrounding 鎖 above it. The first one is easy, but for the latter two it was slightly difficult for me to play around and get the right answer! I thought a bit more about the math after I solved it, and we can view the left and right rotations as cycles \((1,3,6,4)\) and \((2,4,7,5)\) in \(S_7\), where we number the positions from top to bottom and left to right in order 1 through 7, i.e. 可 starts in position 1, 封 starts in position 2, and 連 starts in position 7.

The first question to ask is if these two elements generate \(S_7\), and the answer is yes! Code is below in Julia. Next, we can ask what the minimum word length is to reach any of the \(7!=5040\) permutations using just these two generators, and the answer is 20. I was curious because God’s number for the Rubik’s cube is 20, and I wasn’t sure how to intuitively estimate minimum word lengths from the number of available generators and number of group elements. If we added inverses (which aren’t in the video game), we find we could reach any permutation in just 14 moves.

Also, if we notice that the characters in positions 3 and 6 are both 的, then we actually find that only 16 moves are required without inverses and just 12 with inverses!

Lastly, when I was working on the puzzle, I ran into a couple situations (when I had a wrong solution in mind that I was aiming at) where only two characters were swapped. I checked how hard this was to do, and it turns out that most swaps in the game require 13 moves with the most requiring 17 moves when not considering the two equal characters. Taking this into account still yields a mode of 13, a high of 14, and several lower numbers. No wonder I had trouble swapping them!

It’s clear that this puzzle could have been much, much harder if the designers willed it! The actual solution was quite straightforward as the characters were aligned to make one think of the right answer and the number of moves required was fairly small.