Simple Markov, Chebyshev, and Hoeffding Inequalities
Published: 28 Feb 2025
Last updated: 29 Mar 2025
Categories TagsHere are simple visuals for the Markov, Chebyshev, and Chernoff inequalities, as well as a connection to Cramer’s theorem and intuition about how to derive the Hoeffding inequality from them.
Markov, Chebyshev, and Chernoff
Let $X$ be a random variable. Using an indicator variable, we have $\Pr\sqbracks{\abs{X-c}\geq a}=\E\sqbracks{𝟙_{\abs{X-c}\geq a}}$. We can recover various bounds/inequalities by considering different values of $c$ and functions $f(x)$ that dominate $𝟙_{|x-c|\geq a}$. By the monotonicity of the Lebesgue integral, we have that $\E[𝟙_{|X-c|\geq a}]\leq \E[f(X)]$.
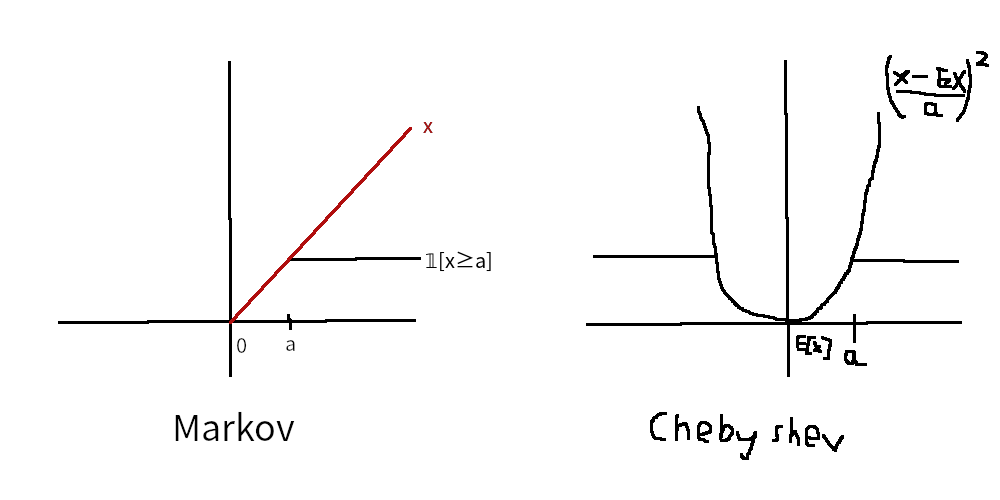
If $c=0$, $f(x)=x/a$, and $X$ is nonnegative, then we get Markov’s inequality as
\[\Pr[X\geq a]=\E[𝟙_{X\geq a}]\leq\E[X/a]=\E[X]/a\]If $c=\E[X]$ and $f(x)=((x-\E[X])/a)^2$ (the quadratic that passes through $(\E[X]+a,1)$), then we get Chebyshev’s inequality as
\[\Pr[\abs{X-\E[X]}\geq a]=\E[𝟙_{\abs{X-\E[X]}\geq a}]\leq\E[((X-\E[X])/a)^2]=\Var[X]/a^2\]With $c=0$ and $f(x)=\phi(x)/\phi(a)$ for $\phi$ nondecreasing and $X$ nonnegative, we get extensions of Markov’s inequality,
\[\Pr[X\geq a]\leq\E[\phi(X)]/\phi(a)\]For example, with $\phi(x)=e^{tx}$, we get the Chernoff bound
\[\Pr[X\geq a]\leq M[t]e^{-ta}\]where $M[t]$ is the moment generating function.
Hoeffding bound and connection to Cramer’s theorem
As an extension of Chernoff’s bound, with $Y_i$ iid and $X=S_n=∑_i(Y_i-𝔼[Y_i])$, we instead get
\[\Pr[X\geq a]\leq M_{X}[t]e^{-ta}=M_{\sum_iY_i}[t]e^{-ta}=\prod_i M_{Y}[t]e^{-ta}=M_Y[t]^ne^{-ta}=e^{n\ln M_Y[t]-ta}\]where $μ(t)=\log M(t)$. This bound (or the variant where we look at the average $\bar{Y}_n=X/n$ to get $\Pr[\bar{Y}_n\geq a]≤e^{-n(ta-μ(t)}$) is useful for thinking about Cramer’s theorem.
We can prove the Hoeffding inequality from this. First, we need the following lemma: For $X$ a random variable with $a≤X≤b$, for any $t∈ℝ$, $\ln M(t)≤t𝔼[X]+t^2(b-a)^2/8$. We can think of this as being related to the Taylor series of $e^{tX}$; $e^{tX}=1+tX+t^2X^2/2!+…$ so $𝔼[e^{tX}]=1+t𝔼[X]+t^2𝔼[X^2]/2!+…$, and taking $\ln$ of both sides, we get
\[\begin{align*} \ln \mathbb{E}[e^{tX}] &= \ln(1 + t\mathbb{E}[X] + \frac{t^2\mathbb{E}[X^2]}{2!} + O(t^3)) \\ &= (t\mathbb{E}[X] + \frac{t^2\mathbb{E}[X^2]}{2!} + O(t^3)) - \frac{1}{2}(t\mathbb{E}[X] + \frac{t^2\mathbb{E}[X^2]}{2!} + O(t^3))^2 + O(t^3) \\ &= t\mathbb{E}[X] + \frac{t^2}{2}(\mathbb{E}[X^2] - \mathbb{E}[X]^2) + O(t^3) \end{align*}\]using the Taylor series $\ln(1+x)=x-x^2/2+…$. This explains where the linear term comes from, and if we look at the quadratic term, we find an intuitive but nonrigorous way to get $8$. We have
\[\frac{t^2}{2}(𝔼[X^2]-𝔼[X]^2)=\frac{t^2}{2}\Var(X)\]and using Popoviciu’s inequality on variances, we know that $\Var(X)\leq (b-a)^2/4$, so overall the quadratic terms are bounded by $(b-a)^2/8$. The fact that higher order terms can also be contained in this bound, and that they give an upper bound is where handwaving comes in. The proof is just a simple optimization problem, but I don’t have any more intuition about it.
From this, we can derive Hoeffding’s inequality by applying the lemma and minimizing the bound in $t$:
\[\Pr[X\geq ε] \leq e^{n\ln M_Y[t]-tε} \leq e^{nt^2(b-a)^2/8-tε}\]We differentiate the exponent with respect to $t$:
\[\frac{d}{dt}(nt^2(b-a)^2/8-tε) = \frac{n(b-a)^2t}{4}-ε\]Setting this equal to 0, we get $\frac{n(b-a)^2t}{4}=ε$ or $t = \frac{4ε}{n(b-a)^2}$. Then plugging this back in, we have
\[\Pr[X\geq ε] \leq \exp\left(\frac{n(b-a)^2}{8}\cdot\frac{16ε^2}{n^2(b-a)^4}-ε\cdot\frac{4ε}{n(b-a)^2}\right) = \exp\left(\frac{2ε^2}{n(b-a)^2}-\frac{4ε^2}{n(b-a)^2}\right) = \exp\left(-\frac{2ε^2}{n(b-a)^2}\right)\]which is the Hoeffding inequality!
An easy generalization of this (which is what is usually listed as the full Hoeffding inequality) is allowing $Y_i$ to have different bounds $(a_i,b_i)$; in that case, the denominator changes to $∑_i(b_i-a_i)^2$.
Sources
- Muni Sreenivas Pydi (ముని శ్రీనివాస్ పైడి)’s answer to What is an intuitive explanation of Markov’s inequality? - Quora
- Source of that Quora post: people.math.wisc.edu/~roch/mdp/roch-mdp-chap2.pdf
- Source of the note about Cramer’s theorem: Large deviations: Cramér vs Sanov - Tim van Erven.
- Source of the Hoeffding inequality derivation: N. Cesa-Bianchi and G. Lugosi, Prediction, learning, and games. Cambridge University Press, 2006.
- An alternative visualization of the Markov inequality: probability - Visualizing Markov and Chebyshev inequalities - Mathematics Stack Exchange